Many people find mathematics daunting. If true, this piece is for you. If not, this piece is still for you.
What do you think of when you think about mathematics? Perhaps you think about x’s and y’s, intractable fractions, or nonsensical word problems. The cartoonist Gary Larson once depicted hell’s library as containing only giant tomes of word problems. You know, “If a train leaves New York…”
I was trained as a mathematician, and I will let you in on a trade secret: That is not what mathematics is, nor where it lives. It’s true that learning mathematics often involves solving problems, but it should focus on the joy of solving puzzles, rather than memorizing rules.
I invite you to see yourself as a problem solver and mathematician. And I’d like to introduce you to the man who once invited me to the study of problem solving: George Pólya.
Math Pólya’s way
For many reasons, not the least of which is that Pólya died in 1985, you will meet him as I did – through his wildly successful “How to Solve It.” Penned in 1945, this book went on to sell over one million copies and was translated into 17 languages.
As a mathematician, Pólya worked on a wide range of problems, including the study of heuristics, or how to solve problems. When you read “How to Solve It,” it feels like you’re taking a guided tour of Pólya’s mind. This is because his writing is metacognitive – he writes about how he thinks about thinking. And metacognition is often the heart of problem solving.
Pólya’s problem solving plan breaks down to four simple steps:
1. Make sure you understand the problem.
2. Make a plan to solve the problem.
3. Carry out the plan.
4. Check your work to test your answer.
There it is. Problem solving in the palm of your hand – math reduced to four steps.
Here’s a classic problem from research on mathematics education done by Jean Lave. A man, let’s call him John, is making ¾ of a recipe that calls for 2/3 cup of cottage cheese. What do you think John did? What would you do?
If you’re like me, you might immediately dive into calculations, perhaps struggling with what the fractions mean, working to remember the rules for arithmetic. That’s what John seemed to do, at first. But then he had a Eureka! moment.
John measured 2/3 cup of cottage cheese, then dumped it onto a cutting board. He patted the cheese into a circle and drew lines into it, one vertical, one horizontal, dividing the cheese patty into quarters. He then carefully pushed one quarter of the cottage cheese back into its container. Voilá! Three-quarters of 2/3 cup of cottage cheese remained.
John is a mathematician and problem solver. First, he understood the problem: He needed ¾ of what the recipe called for, which was 2/3 cup. Then, he made a plan, most likely visualizing in his head how he would measure and divide the cottage cheese. Finally, he carried out the plan.
Did he check his answer? That remains unclear, but we can check the validity of his work for him. Did he indeed end up with ¾ of 2/3 cup of cottage cheese? Yes, because the full amount was reduced by one-quarter, leaving three-quarters.
Another approach
Would this solution work with different foods or serving sizes? So long as a person could divide that serving into quarters, yes, the plan would work.
Could we solve the problem another way with the same result? Sure — there are many ways to solve this problem, and they should all result in the same half-cup answer. Here is one.
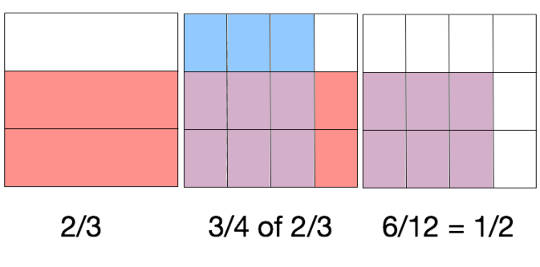
How to find 3/4 of 2/3. Jennifer Ruef, CC BY
Notice that this solution uses pictures. New brain research validates what mathematics educators have been saying for decades: Pictures help us think. Drawing pictures also happens to be another of Pólya’s suggestions.
John probably made use of one of Pólya’s most important suggestions: Can you think of a related problem?
Of course, this is a cheesy problem – sorry, I really didn’t even try to fight that pun – which is a common complaint about story problems. I chose it because it has delighted math researchers for years, and because John is quite clever in his solution. He is also extremely mathematical.
I’ve taught mathematics, and how to teach mathematics, for nearly 30 years. For over a decade, it was my job to convince high school freshmen not only that algebra was meaningful, but that it was meant for them, and they for it. In my work, I’ve met many people who love mathematics and many who find it overwhelming and nonsensical. And so it’s an important part of my work to help people see the beauty and wonder of mathematics, and think of themselves as mathematicians.
These messages are especially important for parents helping children learn mathematics. If you understand the problem you’re trying to solve, you’re well on your way to solving it. And you, yes you, are a problem solver.
![]() We all know it’s not always so simple to solve problems. Pólya did too. That’s the glory of it – the messy, wonderful, powerful adventure.
We all know it’s not always so simple to solve problems. Pólya did too. That’s the glory of it – the messy, wonderful, powerful adventure.
About The Author
Jennifer Ruef, Assistant Professor of Education Studies, University of Oregon
This article was originally published on The Conversation. Read the original article.
Related Books:
at InnerSelf Market and Amazon